片チャンネルのデータを調べてみたら、
再現性はこんなふうだった。
予想だにしなかったので衝撃をうけた。
なぜ、曲がったりするのだろうか、
曲がってしまったときにどう考えたらいいのか悩んだ。
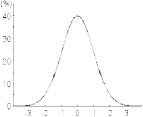
データの統計学的な分布様式が一定であるならば、
その分布を基準にすることができる。
分布を表わす数理モデルを探し、
そのモデルをつかって基準を定義する。
統計学的に、パラメトリックな立場でデータの標準化をする場合にも、
いくつかの流儀がある。
たまたま、ここで紹介する方法は、そのなかの
Exploratory Data Analysis というものに近いステップで進歩してきた。すなわち、
問題があり → データを得 → 分析して → モデルを得 → 結論を得る
というステップで進んだ
(もちろん、いつも教科書どおりではなかったが…)。
論文では、手っ取り早く、まずモデルありきのような説明をした。
けれど、実際にはモデルは探さなければ得られない。
このページでは試みに、進歩をたどるように説明してみよう。
先を急がれる方はこちらへ。
とりあえず片チャンネルのデータの対数値から平均値と相対値を求め、
zスコアを算出した。
モデルの妥当性の検証が甘かった。
測定の再現性が悪かった。
また、とんでもない値のレシオがしばしば観測された。
そうしたレシオは、強く・または弱く発現する遺伝子から
偏って観測された
(そのどちらから観測されるかは、実験ごとで異なった)。
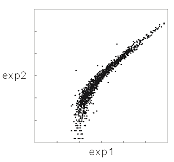
スキャッタープロットで
片チャンネルのデータを調べてみたら、
再現性はこんなふうだった。

予想だにしなかったので衝撃をうけた。
なぜ、曲がったりするのだろうか、
曲がってしまったときにどう考えたらいいのか悩んだ。
曲がらないときもあった。その場合はしばしば、
グラフの左下に「彗星の核」のようなデータの集まりが見られた。
こうした現象は、「バックグラウンド」に関係するのではないか。
そのころすでに、ラボによって(研究者によって)
バックのとりかたには諸説あった。
どれが正しいのだろう?
スキャナーで画像を読み取るときに、
最も小さいシグナルを計測すべく、感度を設定する。
そこで、たとえプローブ分子がない場所でも、
なんらかの値をもつ。
これがバックグラウンドの起源だ。
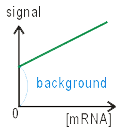
もう少し厳密に言うなら、
スキャンするときには「まったくハイブリダイズがない状態」
についての情報がない。
そこで、シグナルがゼロになるところの機械の校正ができない。
しかし読まぬわけにもいかないから、
なにか適当な値をその場のゼロに仮設定する。
その仮設定された値から、真の値を引いた値が
バックグラウンドである。
そこで、バックは正にも負にもなり得る。
バックグラウンドは実測できない。
スポットの周りを測定して引く場合が多いが、
これは、ある仮定のもとでの作業である。
すなわち、スポットとその周辺で、
おなじ密度でノンスペなシグナルがあるという仮定だ。
実際には、スポットとその周辺では、物性が違う。
そこで、先の仮定は合理的でない。
また、バックの主原因はフリーの色素だが、
これの含まれる割合は実験ごとに異なる。
そこで、経験による推定の補正も不可能だ。
しかし、バックを無視してはいけないのは明らかである。
これもひとつの手段だと紹介したレビューがあったが、
冗談じゃない、それはとんでもないことだ。
そんなことをしたら、レシオの信頼性が台無しではないか。
わからないが重要なものは、未知数として扱い、
それを解く努力をすべきである。
バックグラウンドを未知数として、
対数正規分布モデルを組むとこのモデルになる。
式はこちら。
いつの日にか、式の意味するところについて説明したいと思うのだけど、
それは私の任ではないような気もする。
じつは、アレイデータの対数値は、
どんな分布モデルとも一致しない。
強いていうと、どちらかに偏った正規分布をする。
モデルと実際の値が一致しないときにすべきことは、
厳密に一致するかどうかは、
normal probability plot というグラフで判断する。
通常、このような図になる。
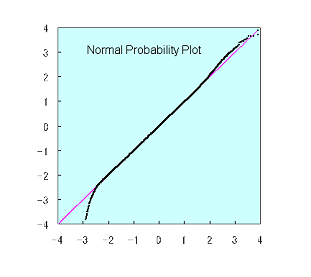
もしモデルがデータと一致すれば、y=xのプロットになる。
データのほとんどの領域はモデルと一致する。ただし、
最も強いシグナルの領域と、最も弱いシグナルの領域は、
モデルと一致しない。
それぞれ、シグナルの飽和と、相和的ノイズの影響によるエラー
であると考えられる。
実際、これらの領域のデータには再現性がない。
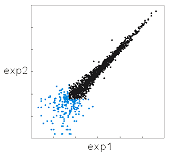
かように改善された。曲がってもいないし、
彗星のようでもない。
ただし、青いスポットはモデルと不一致な領域で、
そこではデータに再現性がない。
持ち込まれた・探して入手した、ほとんどのデータの分布が、
このモデルと一致した。
いくつかの、救いようがないほどノイズレベルの高い例外はあったけれど。
プラットフォームとは関係ない。
マイクロアレイでなくてもいい。
何例のデータを調べたかは、もうわからない。
500例くらいまでは数えていたが、やめてしまった。
一致するのにはたぶん原因があり、
その原因は細胞のしくみに由来しているようだ。
これについては理論を説明する論文を投稿中である。
(サイトは準備中---というより、その論文の審査待ちの時間が今で、
どんどん書いているのだけど、なかなか終わらない)。
標準化は、チャンネルごとに行われる
(アフィメトリクスのように、単チャンネルなら、その実験ごとになる)。
別の実験や、チャンネルのことは考慮されない。
だから、どんなレシオが出てきても不思議ではない
---もう少し正確に言うと、この方法は、レシオについては、
値を変える手段を持っていない。
しかし、このように自然に、
一定のレシオ巾が、どのシグナル強度でも、得られてくる。
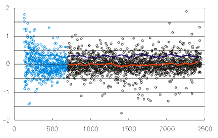
このrank-logratio plotは、x軸は2つのチャンネルのシグナル和のランク、
y軸はシグナルのレシオ対数値を表わす。
青い部分は、モデルと不一致なシグナル領域である。
一見して、レシオがシグナル強度とは無関係に、
一定の分布をすることがわかる。実は、どこの強度域でも、
(金太郎飴のように)レシオ対数値はおなじ分布---正規分布---をしている。
これは、ずっと仮定されていた性質が確認されたということでもある。
遺伝子の変化はレシオで考えていいし、どんな(強い・弱い)遺伝子でも、
レシオを共通のモノサシに使ってかまわない。
データはzスコアで得られる。
しかも、その差が正規分布する。
そこで、ガウスモデルに準拠した扱いをすればいいことになる。
もちろんレシオで考えてもいい。
zスコアの差はいつでもレシオに変換できる。
やや詳しい解説はチュートリアルを参照されたい。
もっと詳細な解析については、次の論文のアクセプトをお待ちください。
(株)スカイライト・バイオテックのサービスが利用できます。
かれらのコンタクトページから連絡してみてください。
この標準化の方法にはSuperNORM©という名前がついております。
もろもろの、特に経済的なところのメリットについては、
ホームページをごらんください。
特に断らない限り、ここではlogの底は 10 である。
これは計算の標記上の複雑さを増加させる原因で、実際、
(そのせいだけではないのだろうけど)論文の標記ミスを誘った。
しかし自然対数を使わないのは、
ひとえに、
真数を想像できないからだ。
ひごろ使う際には、積分なんかしないのだから、
常用対数の方が便利だ。
インフォマティシャンの多くは、
底として 2 を使いたがるようだ。
情報量をビットで表わしたいからだろう。
しかし私は生物屋なので、1024だの256だのといった数に郷愁はなく、
もちろん私の同僚たちにもない。
1000なら3、2なら100、これなら見当がつく。
もちろん、底はzスコアや、レシオの値には影響しない。
しかしσパラメーターには影響する。
紛らわしいので、皆さんの御協力をお願いします。
対数の底は10で標記しましょう。
こう書いておきながら、このところ、発現の触れ巾を表すときにだけ
2を使っています。それはなぜか。
ふたつの理由があります。ひとつはそれがすでに浸透しているからで、
10を使うと妙な間違いの元になりかねないからです。
もうひとつは、じつは2倍というのが、遺伝子の変動を表すのに手頃なのです。
10倍動くケースは珍しい。すると、底を10にすると、多くのログレシオ値は
1から−1の間になります。さて、0.7は真数だと何倍だったでしょうかね?
というわけで、ことこれに関しては、もっと小さい数を底にしたほうが、
感覚的にわかりやすいのでした。1より大きい、最も小さい整数だから2。
標記するときにlogでもlnでもなく、log2と書かねばならんのが
面倒ですけどね。
| Go Back | Home | Transcriptome Home |
 |