3パラメータモデルによる標準化
これは短いバージョンのページです。冗長でも詳しいほうがいい方は
こちらをどうぞ。
原理
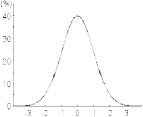
一般に、測定値は分布する。その分布様式が数式で定義できるとき、
その数式を標準化のための基準として使うことができる。
マイクロアレイを含むトランスクリプトームデータの分布様式は一定で、
3パラメータ対数正規分布モデルで表わすことができる。
この分布を基準として、データの標準化をする。
正確なモデルによる標準化
3パラメータ対数正規分布モデル
測定のバックグラウンドを未知数として、
対数正規分布モデルを組むとこのモデルになる。
式はこちら。
このモデルそのものは、わりと一般的なもので、
統計学の教科書にも載っている(こともある)。
モデルの妥当性の検証
データの分布様式を簡単に確かめるためには、ヒストグラムを用いる。
しかしもっと厳密にモデルとデータが一致するかどうかは、
normal probability plot というグラフで判断する。
もしモデルがデータと一致すれば、y=xのプロットになる。
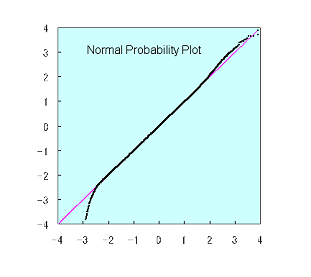
マイクロアレイの場合、通常、このような図になる。
マイクロアレイデータのほとんどの領域はモデルと一致する。
ただし、最も強いシグナルの領域と、最も弱いシグナルの領域は、
モデルと一致しない。
それぞれ、シグナルの飽和と、相和的ノイズの影響によるエラー
であると考えられる。
実際、以下に述べるように、これらの領域のデータには再現性がない。
標準化したマイクロアレイ測定の再現性
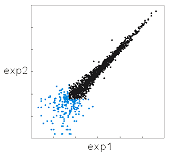
良好な再現性が得られた。
ただし、青いスポットはモデルと不一致な領域で、
そこではデータに再現性がない。
モデルの普遍性について
持ち込まれた・探して入手した、ほとんどのトランスクリプトームデータの分布が、
このモデルと一致した。
実験のプラットフォームとは関係ない。
実は、マイクロアレイでなくてもいい。
なぜこの数理モデルはデータと一致するのだろう?
一致するのにはたぶん原因があり、
その原因は細胞のしくみに由来しているようだ。
これについては理論を説明する論文を投稿中である。
測定したレシオとシグナルの強度の関係
標準化は、チャンネルごとに行われる
(アフィメトリクスのように、単チャンネルなら、その実験ごとになる)。
この方法は、レシオ値を変える手段を持っていない。
しかし、このように自然に、
一定のレシオ巾が、どのシグナル強度でも、得られてくる。
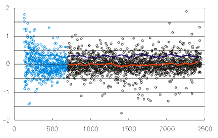
このrank-logratio plotは、x軸は2つのチャンネルのシグナル和のランク、
y軸はシグナルのレシオ対数値を表わす。
青い部分は、モデルと不一致なシグナル領域である。
レシオはシグナル強度とは無関係に、
正規分布をしている。
これは、ずっと仮定されていた性質が確認されたということでもある。
遺伝子の変化はレシオで考えていいし、どんな(強い・弱い)遺伝子でも、
レシオを共通のモノサシに使ってかまわない。
標準化したマイクロアレイデータをどう比較すればいいか
データはzスコアとして得られる。
しかも、その差が正規分布する。
そこで、ガウスモデルに準拠した扱いをすればいいことになる。
もちろんレシオで考えてもいい。
zスコアの差はいつでもレシオに変換できる。
やや詳しい解説はチュートリアルを参照されたい。
もっと詳細な解析については、次の論文をお待ちください。
その標準化を試したいのなら
(株)スカイライト・バイオテックのサービスが利用できます。
かれらのコンタクトページから連絡してみてください。
この標準化の方法にはSuperNORM©という名前がついております。
もろもろの、特に経済的なところのメリットについては、
ホームページをごらんください。
original:04 Jan 2005; updated:1 Feb 2005
小西智一
秋田県立大学
生物資源科学部/地域共同研究センター