データの比較

ふたつ以上のサンプルがあるとき、ある遺伝子の発現量を比較することができる。
サンプルごとに標準化されたデータはz-scoreになっている。
z-scoreは普遍的な値である（standard unitという単位を考えることができる）。
そこで、これらは比較可能である。具体的には下記に述べるように、差をみることになる。

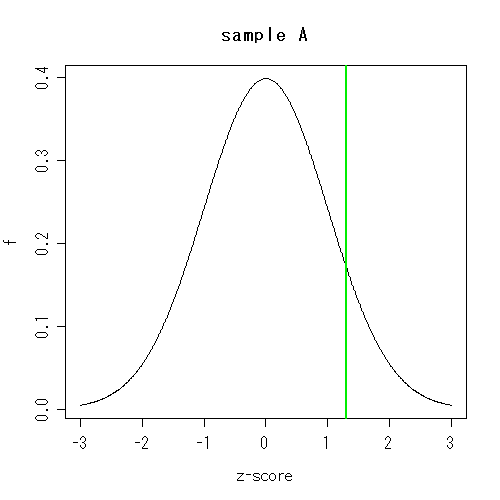
たとえばここに、サンプルＡとＢがある。
それぞれの測定値は、サンプルごとに遺伝子発現の集団のなかで標準化されている。
そのなかのある遺伝子に注目したところ、サンプルＡでは1.3、Ｂでは-0.5であった。

これらの違い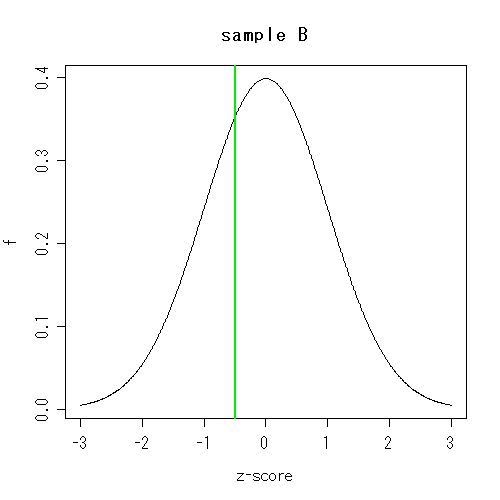

熱力学モデルによると、z-scoreの違いは、それぞれの差で考えればよいことになる。
それぞれのmRNAの量は、ゲノムDNAと種々の因子の相互作用によって決定されている。
個々の相互作用は自由エネルギーのかたちで表すことができ、
相互作用の総量は（エネルギーなので）総和で表される。
この総和と、個々の発現量を表すz-scoreはリニアな関係にある。

そこで、なんらかの因子（群）が原因となってあるmRNAの量を増減させたとき、
その変化した自由エネルギーの大きさは、
変化前と変化後のz-scoreの差から求めることができる。

kは比例定数だが、現時点ではこの値の大きさは不明。

上記の「原因」の単位はstandard unitであるので、そのまま一般性を持つ。
そこで、より高度な作業は、この値を用いて行えばいいことになる。

ふたつのサンプルA,Bの測定結果における、ある遺伝子の発現量の比とz-scoreの差は、
次のような関係をもつ。
log₁₀([gene_A]/[gene_B]) = σ(z-score_A - z-score_B) （-> 論文)
ふつうログレシオの底は2にするので

そのとおり。

熱力学モデルによるとこう説明される。
それらの違いは、細胞内の調節因子の活性濃度の変化によってもたらされている。
活性濃度の違いは自由エネルギーの違いを、
そして自由エネルギーの違いはz-scoreの差をもたらす。
そこでz-scoreの差は、いつも一般性をもって扱うことができる。

プロテオームで考えるなら、これらのトランスクリプトームの変化は、
タンパクのモル濃度を同じだけの割合で変えていると考えられる。
他の条件が等しければ、活性濃度も同じ割合で変わっているはずだ。
ならば、反応速度も同じ割合で変わるだろう。

測定にともなうノイズやエラーのうち、相乗的なノイズは、
z-scoreに相加的に影響する。

このノイズ成分noize₁-noize₂は正規分布すると考えられるので、
これの影響は、繰り返し測定をパラメトリックな統計手法で扱えば、コントロールできる。

一方、そのほかのノイズやエラー（相加的なものや、バックグラウンド）は
リニアでない影響をするため、簡単には影響がコントロールできそうにない。
いわゆるノンリニアな扱いが必要になるが、これを扱うためのノンリニアなモデルはまだ用意されていない。
もちろん、不適切なモデルを使えば間違いのもとになるだろう。
影響をうけるデータはあらかじめ区別できるのだから、そうするべきだろう。

生理学的な違い、個体差や、なにかちょっとした環境の違いによる変動は、
熱力学モデルによると、z-scoreに相加的に影響すると考えられる。
こうした変動は、因子の活性濃度を相加的に変化させるだろうからだ。
実際、マイクロアレイで観測される変動の主要因は正規分布で表される（-> 論文)。
こうした生物学的な小さな違いもz-scoreに相加的に影響し、その総和は
おそらく正規分布するだろう。

以上から、標準化の際に除くことができないノイズ（相乗的なノイズおよび生物学的なノイズ）
は、測定結果に相加的に働き、概略で正規分布することが期待される。