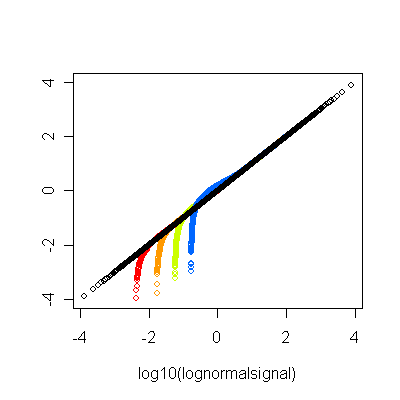
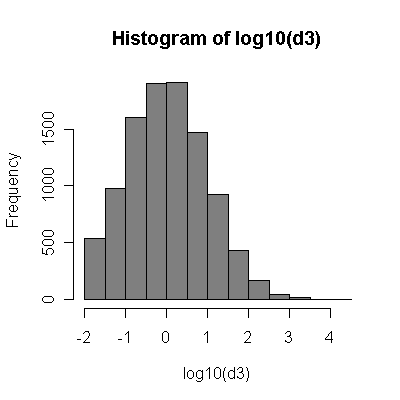
よく使われる分布の確認方法にヒストグラムがある。
ぱっと見で特徴をつかみやすい利点があるけれど、やや厳密さに欠ける。
どんなヒストグラムが何を表すのかがわかりにくいからだ。
もっと厳密に確認するための図示の方法にQ-Q Plotがある。
これは、1対のデータセットの分布が同じなのか違うのかを確かめる方法である。
それぞれのデータセットの同じ分位数(パーセンタイル等)を比較する。
もし分布が一致するなら、当然、同じ分位数は一致する。
上位1, 2, 3, ... 99, 100パーセンタイルの人々の年収はおよそ一致するだろう。
そこでQ-Q Plotは y=x の直線になる。
Q-Q Plotを使って、ある実験データを数理モデルと比較することもできる。
たとえばデータを正規分布(という数理モデル)と比較すれば、
そのデータが実際に正規分布するのかどうかはまさに一目瞭然になる。
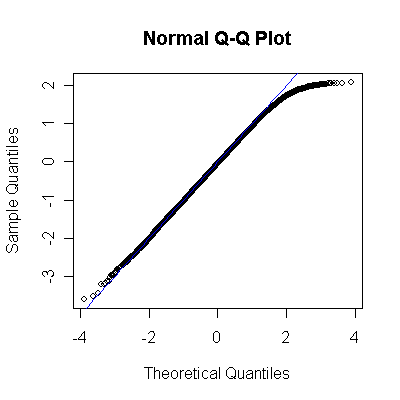
この用法はよく Normal Q-Q Plot ないし Normal Probability Plotとして紹介されている。
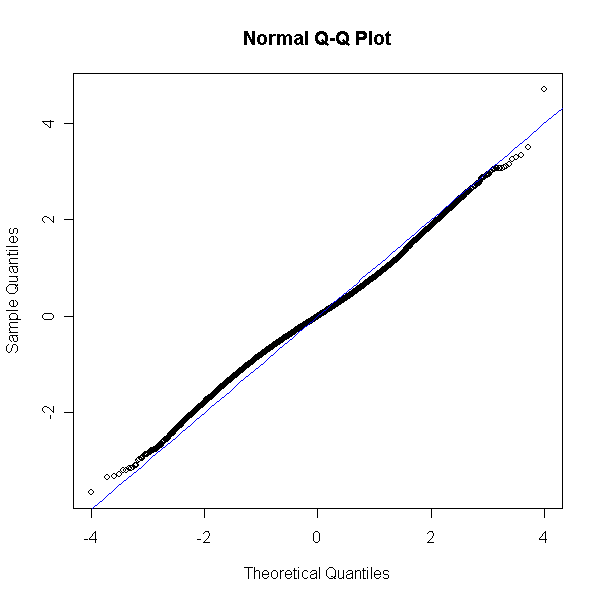 |
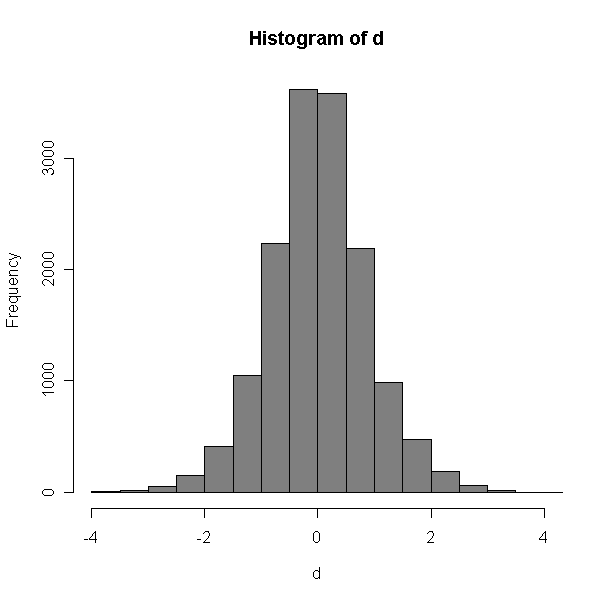 |
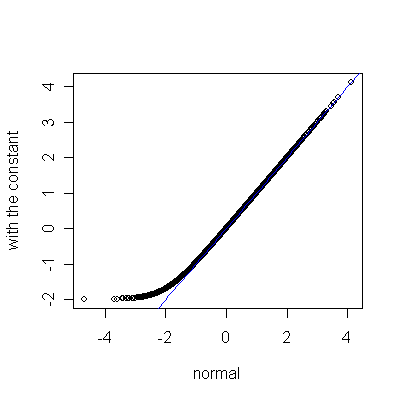
ヒストグラムではわかりにくいが、 Q-Q Plotでは直線からのずれが確認できる。
どうしてもゼロ付近が混んで、そこから離れるほど疎になる。
もともとゼロから離れたデータはとても珍しくなるのだが、
そうしたデータがしかし(印象として)目立つところに図示されることになる。
しばしば、プロットの端はさまざまな理由で直線を外れるけど、
どのくらいの割合のデータが実際に外れているのかは確かめるべきだろう。
 しかもその関係はリニアではない。
しかもその関係はリニアではない。