ratio_supplement

それぞれのサンプルで標準化する、とは

これらの違い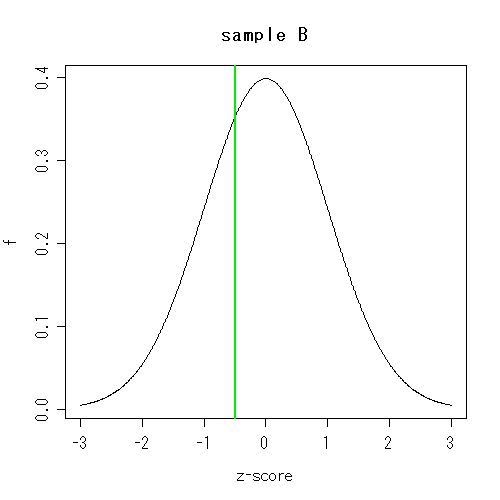

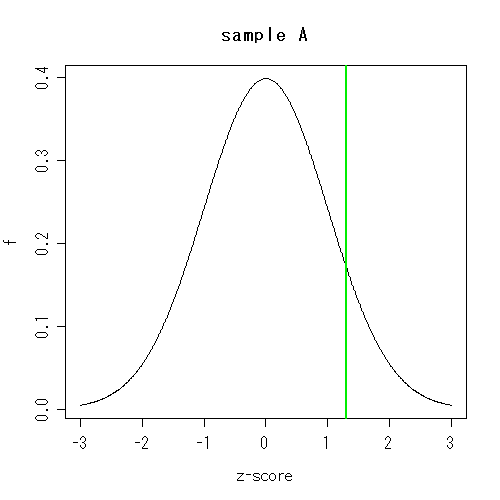
これらのサンプルは両方とも、遺伝子発現のレベル（の対数値）が正規分布している。
標準化された遺伝子発現のレベルはz-scoreで表される。
このスコアは、平均が０で、標準偏差が１になる性質を持っている
（その分布を示しているのが実線で書かれたヒストグラムだ）。
同じ遺伝子のスコアはサンプル間で直接に比較できる。

ここで一つの仮定をしている。
これらのサンプルの母集団の性質が同じであるか、同じであると見なせる、という仮定だ。

母集団の性質は同じか？

どちらも（測定の目的にもよるが、おそらく同じ種類の細胞の）mRNAの集団である。
これらは細胞を形成する基盤であるから、
本質的に異なることはたぶんないだろう。
おそらく分布中心は同じモル濃度になるだろう。
また分布の幅も同じだろう（こちらは多くの測定結果から支持されている）。（-> たとえば、この論文の例)

分布中心を実際に知るのは現時点では困難だ。
しかし仮に、分布中心のモル濃度が異なっていたとする---
細胞の種類が違うのならこれは有り得ることかもしれない^*。
こうした場合、データを比較する目的は何になるだろう？
おそらくその目的は、
「ある遺伝子が、それぞれの細胞にとって、どんな役割を果たしているかを知ること」
「その役割がサンプル間で異なっているかどうかを知ること」
であろう。

トランスクリプトームはプロテオームを決定する。
そこで、ある遺伝子の役割は、その発現量が他の遺伝子の発現量という母集団のなかで、
どんな位置にあるのかによって決まるだろう。
これが妥当な推定であるなら、それぞれの母集団の性質は実質的に同等だと考えて良いことになる。

^*タンパクの新陳代謝が低い組織なら、mRNAのモル濃度は低くてもかまわない。
プロテオームを保ちながら新陳代謝を下げるためには、タンパクの分解速度と合成速度とが等しく下がればよい---
たとえば、ある状態からそれぞれ半減させれば、プロテオームを保つことができる。
mRNAはタンパク合成のための鋳型であり、おそらく合成速度はこのモル濃度に比例する。
そこで、全てのタンパクの合成速度を半減させるためのもっとも単純な方法は、
mRNAのモル濃度を半分にすることだ。
新陳代謝を低くすれば、急激な変化に迅速に対応できないものの、省エネルギーな運用が可能だ。

ただ、細胞が実際にこのように合目的にできているかどうかはわからない。

細胞に含まれるRNA量は一定か？

上記に似た設問だが、この答えは否である。
対数正規分布する数列の和は不安定だからだ。
たぶん、もっとも強い発現を示す数種類の遺伝子が発現を変えれば
全RNA量は影響される。
これは、全RNA量でデータを標準化できないことの（原理的な）理由である。
一定な性質が期待されるのは分布の中心であり、それは
物理的な存在ではない。

同じサンプル内の、異なる遺伝子のz-scoreは比較できるか？

できるが、感度補正が必要になる。
現時点ではz-scoreは（モル濃度＋感度）を表している（-> 論文Konishi 2008a）。
この感度はスポットとウエット実験の条件によって決まる定数である。

発現量の違い＝（変化後モル濃度＋感度_spot1）- （変化前モル濃度＋感度_spot2）

そこで、同じスポットでの発現量の違いを求める際には、感度は相殺される。
しかし異なる感度をもつスポット間ではいつも感度_spot1-感度_spot2という決まった違いを生じる。

z-scoreの差

多くのケースで、正規分布する数は、それぞれが多数の要素の和なのではないだろうか^*。
試験の場合は、才能や努力や山勘、といったものが、
それぞれ回答結果に相加的に働くから正規分布するのだろう。
体重の場合は、「そこでもうひとくち食べるかどうか」等が相加的に脂肪を....

^*厳密にはこれは逆。
多数のiidランダムな数の和からなる数列は正規分布する。(中心極限定理）
この定理は、「正規分布する全ての数列が、もともとiidランダム数の和である」とは述べていない。

そうした多数の和から成るケースでは、違いの原因を抽出するためには
差をとればいいことになる。

z-score_A + 原因＝ z-score_B

そこで、偏差値60と50の違いは60-50=10。これは50と40の違いと等価である。

極端なz-scoreについての例外？

とはいえ、3が4になるときはどうなのか？　となると、別の問題が生じるかもしれない。
この点も、偏差値90と80はどう違うのかと似た問題かもしれないのだけど、
iidランダムの和という前提から外れるかもしれない。
つまり、要素としてのリソースが限られてくる---
偏差値で説明するなら、試験を受けるのはヒトであって、
その才能はたぶん有限で、
努力をしようにも人生は有限である---という制約を受けている。
細胞のなかでも、RNAにわりふることができる元素の量は有限である。
あまり突出した遺伝子発現は、
リソースの制限を破るための別の仕組みを持つ可能性がある。

試験の結果はしばしば正規分布をするけれど、
収入は決して正規分布せず、上に開いた分布になる。
たぶん能力と収入とはリニアな関係にはない。
これと似た現象は細胞にもあるかもしれない；
妙なアナロジーに頼りすぎると間違えるのだけど。

log(ratio)の底はいつも2に

もちろん底の値が変わると対数値が変わる。はっきりさせておかないと間違いのもとだ。
あらゆる論文がlog(ratio)の底には2を用いている。だからこれに関しては2を使うべきだ。
実際のところ、2倍というのは、トランスクリプトームを扱う上で手頃な値である。

マイクロアレイデータの生データを扱うときは私は10を使っている。
これは下記のσの数値にだけ影響する（z-scoreは無関係）。

洗いの条件と分布の巾を表す　σ

この値はほとんどのケースで0.6から0.8程度になり、測定内で安定である。
とはいえウエットプロトコールによって変化しうる。
おそらくその理由は、ハイブリダイゼーションの洗いの段階にある。
あまり厳しく洗うと大きくなるものと考えられる。(-> 論文)

σが異なるデータを比較するときは、log(ratio)で考えるよりもむしろ
z-scoreの差を使うほうが（σを補正しないほうが)よくデータが一致するだろう。
（目立たないけど）この論文でも結果がそうなっている。
これはつまり、洗いをきびしくしたマイクロアレイデータは、
レシオが強めに観測されるだろうからだ。

洗いをきびしくするのは、まだ定量性が問題にならず、むしろ
印刷画面でのコントラストをはっきり見せたかったノザン法の時代には
便利なテクニックだった。でも、マイクロアレイには不向きである。
ダイナミックレンジが不必要に拡大するからでもあるし、
多くの遺伝子が測定不能になるからでもある。
どんなに厳しく洗っても、識別性能は向上しない。(-> 論文)
洗いはマイルドかつ短時間が望ましい。

ノイズの影響

相乗的なノイズ

生データx_{chip, gene}に掛け算的に働く。

x_{chip, gene} = signal_{chip, gene}× multiplicative_noise_{chip, gene}

このx_{chip, gene}を標準化すると

z-score_{chip, gene} = {log₁₀(x_{chip, gene})-μ_chip}/σ_chip
= {log₁₀(signal_{chip, gene}) + log₁₀(multiplicative_noise_{chip, gene}) -μ_chip}/σ _chip

というわけで、このノイズはz-scoreのなかではシグナル成分にたいして相加的である。
だから二つのz-scoreの差のなかでも、これらは相加的である。

相加的なノイズ

生データx_{chip, gene}に足し算的に働く。

x_{chip, gene} = signal_{chip, gene}+ additive_noise_{chip, gene}

z-scoreの差はlog(ratio)に比例するので、

z-score_{1, gene}- z-score_{2, gene}
∝ log₂ { (signal_{1, gene}+ additive_noise_{1, gene}) / (signal_{2, gene}+ additive_noise_{2, gene}) }

ノイズ成分は割り算の分母にも相加的に働いているので、レシオをリニアでない方法で変動させることになる。
当然、ログレシオへの影響もリニアではない。

データの比較