

Results between 2011 and today
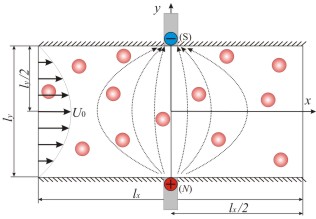
We have investigated the
behavior of magnetic particles between the
two parallel walls in a
non-uniform applied magnetic field situation.
Magnetic particles will
move into the region on this macroscopic flow
through the upstream boundary
surface, be attracted around each
magnetic pole under the non-equilibrium
magnetic field, or move in
the downstream direction without being attracted,
and move out of
the simulation area thorough the downstream surface.
This simulation may be an advancing
simulation in which the Brownian motion is activated by means of the
viscosity-modified
procedure and the multi-body hydrodynamic interactions
are taken into account.
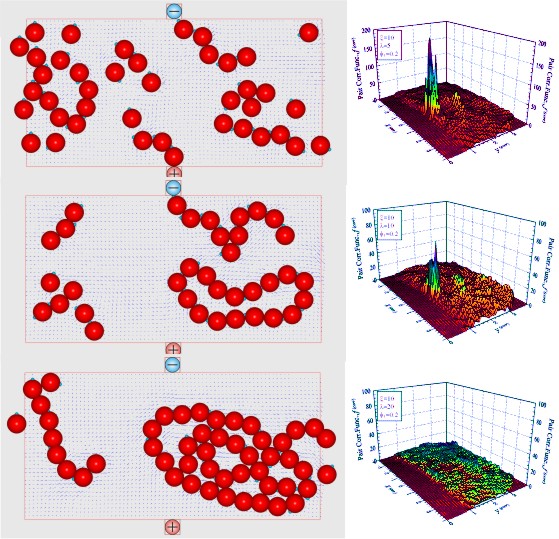
For the case where the magnetic field is
equal to the
influence of the magnetic interaction between
particles,
some clusters are formed in a loop-like formation
and
move in the downstream direction without attachment to
the magnetic
poles and some clusters are formed in a
long chain-like formation with the
end particles anchored
around the magnetic pole.
For the case where the
magnetic interaction between
particles is
significantly dominant, large packed clusters
and chain-like clusters are
formed and flow in the
downstream direction without attachment to
the
magnetic poles.
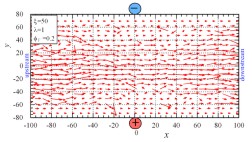
In order to apply the lattice Boltzmann method to a flow problem of
magnetic suspensions, we
have investigated the feasibility of the
viscosity-modifying method that is expected to be a technique
for
sophisticating the activating method of the particle Brownian motion based on
fluctuation
hydrodynamics.

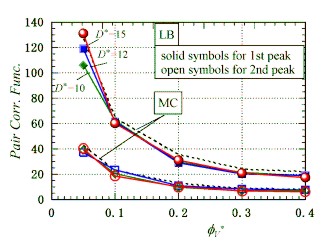
The
figures on the left-hand side are for a very weak applied
magnetic
field and those on the right-hand side are for a very
strong applied magnetic
field.
The snapshots at a lower position are obtained for a
stronger
applied magnetic field.
In the case of a weak
magnetic field, network-like clusters are formed, and in the case of a strong
magnetic field, chain-like clusters are formed in the magnetic field
direction. These aggregate structures are in good agreement with those of
the Monte Carlo method.
We may conclude that the lattice Boltzmann
method with the viscosity-scaling procedure is quite a possible technique for
simulating a flow problem of magnetic particles under a non-uniform applied
magnetic field.
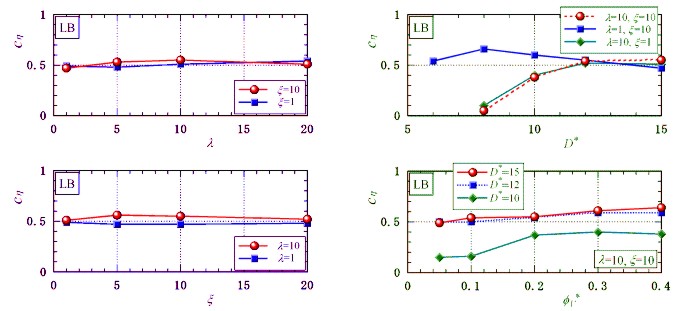
The modified viscosity is almost constant and
independent of the strengths of magnetic particle-field and particle-particle
interactions, and the variation of the volumetric
fraction.
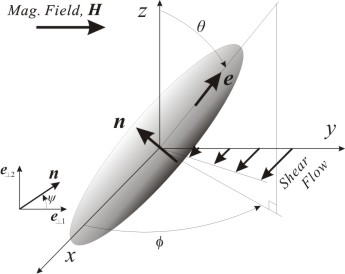
As a model of
the oblate hematite particles that are generated experimentally, we use the
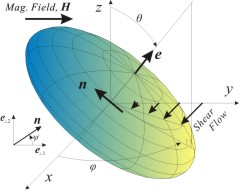
oblate spheroidal particle shown in Fig.1. The particle is assumed to have a
magnetic moment normal to the particle axis at the particle center.
As a model of
the rod-like hematite particles, we use the prolate spheroidal
particle shown in Fig.1. The particle is assumed to have a magnetic moment
normal to the particle axis at the particle center.
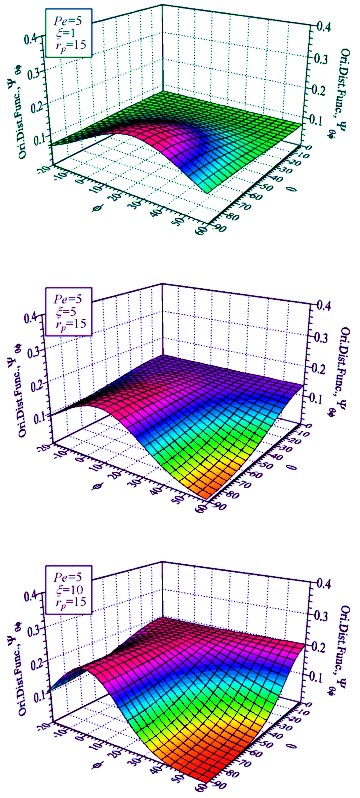
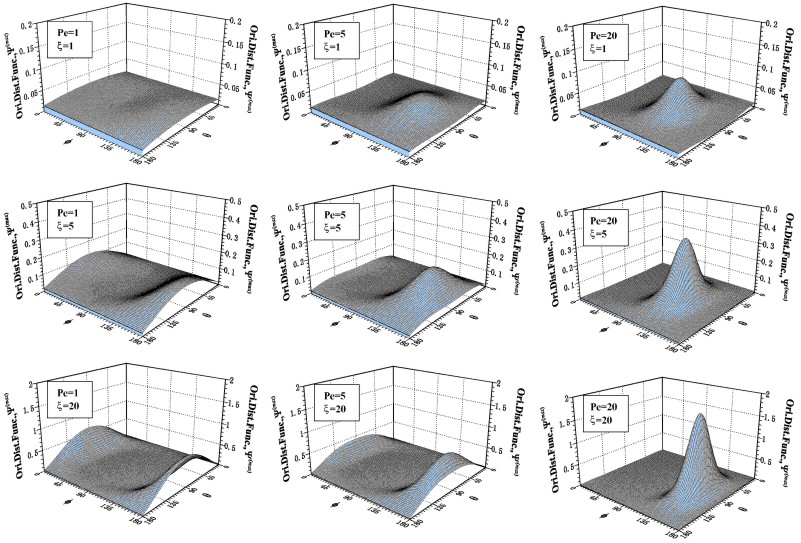
The orientational distribution has a one-peak type shape
for a weak magnetic field, and comes to have a linear-peak type shape with
increasing magnetic field strength.
(a) For a significantly weak
magnetic field
One-peak type distribution.
(b)
For a magnetic field with medium field
strength
(c) For a significantly strong
magnetic field
A linear-peak type
shape
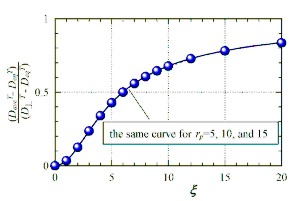
The spin rotational Brownian motion does not
influence the shape of the orientational distribution.
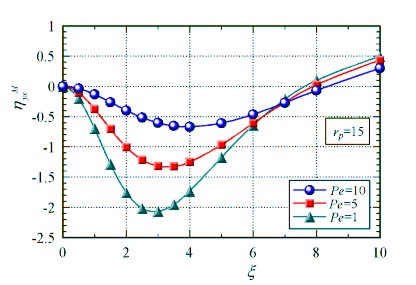
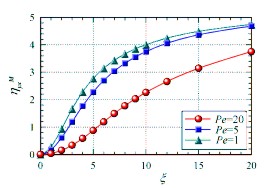
The viscosity
becomes NEGATIVE with increasing applied magnetic field strength as predicted by
the theory without the
spin rotational Brownian motion.
The
spin rotational Brownian motion has a quantitative effect on
the negative
viscosity, although the dependence of the negative
viscosity on the magnetic
field strength is in qualitatively good
agreement with that of the theory
without the spin rotational
Brownian motion
The effect of the spin
rotational Brownian motion quantitatively
appears as a significant decrease
in the negative viscosity
effect.
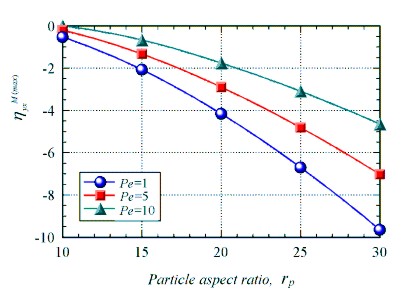
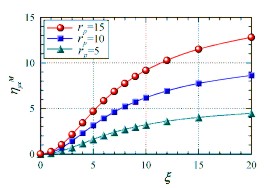
The negative magneto-rheological effect can be obtained
for
a larger aspect ratio or for a more prolate hematite
particle.