階層型クラスタリングによる視覚化

遺伝子群や、実験間の関係を考えるときに、ちょっとその関係を視覚化できると考える助けになるだろう。
クラスタリングはこのための方法である。
考え方として、「似たものを集める」方法と、「集団を区切る」方法がある。
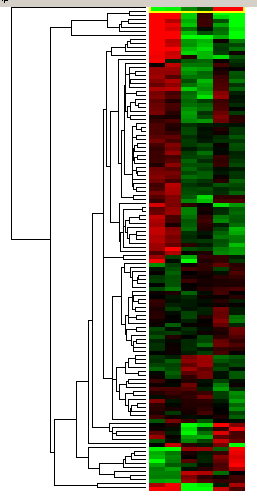
階層型クラスタリングは前者であり、似ているものをグルーピングしたデンドログラムを出力する。→

測定値のｚスコア、またはその平均からの差とって、
そのひとつひとつの中から最も近いもの同士をクラスターにして平均をとり、
その平均と最も近い次のクラスターとをまとめて平均をとり、...
そして最終的にひとつのクラスターにまとめるまで計算をする。

「集団を区切る」方法であり、k-means法や自己組織化写像SOMなどの方法がある。
De Hoonさん作のclusterというソフトウエアでも実行される。
実験間の関係を視覚化する、という目的ではあまり使わないかもしれない。

当然、クラスタリングの結果は、遺伝子発現の違いをどう考えるのかによって変わる。
ある遺伝子1のプローブについて、ｚスコアに標準化された２つのデータ、
サンプルA ₁とサンプルB ₁の違いは、差で考えればいい。

この値は、トランスクリプトレベルのログレシオに比例すると考えられる。
ところが、クラスタリングで扱うのはそのひとつの遺伝子ではない。
測定される遺伝子は複数あるので、それらをどう合算すればいいのかは、ちょっとした問題である。
つまりサンプルAとサンプルBの違い（ないし距離）を、各遺伝子の差からどう考えるかだ。

さらに、それらのサンプルは集められてクラスタをつくる。
各クラスタ間の距離をどう考えたらいいだろう？

ひとつひとつの遺伝子発現の増減を全て直交した次元での出来事として考えるのなら、
サンプル間の距離はユークリッド距離で表せばいいだろう。
ちょうど、たとえば三次元座標のなかの２点間の距離を表すように。

さて、クラスタリングの対象は全ての遺伝子ではないことが多い、
むしろ何らかの観点で選択されているのが普通である
（それに、各チップのコンテンツは、そもそも微妙に異なっている）。
単純なユークリッド距離を使用すると、
対象とする遺伝子数に距離が依存することになる
（遺伝子数が増えると距離も遠くなる）。
その結果を標準化するためには、２乗和をデータ数で割って平均をとればいい。

さて、実際には各遺伝子の発現は独立しておらず、
たぶん一桁か二桁くらい小さい数のタンパク質因子によって制御されている。
しかも、マイクロアレイで比較しようとしているような二つの条件の間では、
そんなに多くの因子が変わっているわけではないだろう
（たいてい、ちょっとした条件の差のもとで測定・比較するからだ）。

もし、たった一つの因子が起こした変化を、
その因子に制御されている遺伝子群だけから推定するなら、
１次元のcity-block distanceで考えるべきだ。
遺伝子を絞った状態でクラスタリングをするときがこちらに相当するだろう。
もちろん、この場合も遺伝子の数で標準化するべきである。

遺伝子差をまとめたサンプル間差をどうまとめるか。
それぞれのサンプルのaverageないしmedianを使えばいいのではないか
と思う...が、これはアレイデータにつきものの生物学的なノイズ（個体差）
を考慮することができなくて、最初の足が長くなってしまう。

ノイズの考慮ということではWard's method が推奨されているようだけど
距離が分散（というか二乗和）で定義されているので、
距離ではなくて面積になってしまうので、そのままでは使えない。

ゴメンナサイ、この件は現時点で考え中です。
とりあえずaverageで出しています。

Rを使わないなら：
De Hoonさん作のclusterと、 EisenさんのTreeViewの組み合わせで計算できる。