標準に用いるRNAを用意して、
それをどちらかのチャンネルに用いるか、あるいは独立して測定しておく。
全てのデータについて、その標準の測定値とのレシオを算出する。
求められたレシオが一定の条件を満たすように、
そのレシオを、非線形の関数を使って補正する。
標準に用いるRNAを用意して、
それをどちらかのチャンネルに用いるか、あるいは独立して測定しておく。
測定したシグナル値を一定の式で処理し、
その標準の測定値との関係をあらわす、ある値を算出する。
その値が一定の条件を満たすように、データを補正する。
補正には関数ではなく、固定したパラメータが用いられる。補正の式は非線形である。
全ての測定値を用いて平均(重心)を計算する。
測定値の対数値を、それぞれが重心に最も近づくように、
一次関数で補正する。
多くの方法が考案されているために、網羅するのは困難である。
しかし、パッケージプログラムとして販売されているもののほとんどは、
(チップメーカーの提供する方法を含む) ノンリニア法に準拠している。
そこで、まずその方法について概説する。
常に、基準と、測定するものとを、2つ並列に比べる。
測定したレシオが、シグナル強度によって一定の傾向を持たないように、
シグナルの平均値の関数によってレシオを補正する。
それはちょうど、でこぼこに曲がったランク−ログレシオプロットを
平らにするような作業である。
(ランク−ログレシオ プロットによる実例)
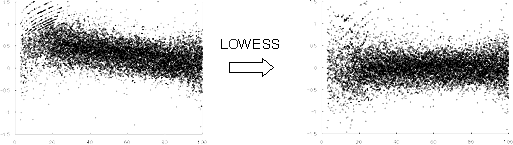
x軸は2つのチャンネルのシグナル和のランク、
y軸はシグナルのレシオ対数値を表わす。
処理前はレシオが一定せず、
シグナルが低いほどレシオが上昇する傾向があるが、
処理後はy=0付近で安定する。
とはいうものの、そうなるように補正関数を仕組んだのだからこれはアタリマエ。
y軸方向のプロットの巾が一定しない問題は残っている。
もう一つ関数を仕組めば解決できるが、さすがにそこまではしなかったようだ
(しかしこの第二の関数の萌芽は、あるレビューのなかに読み取れる。
そのうちだれかが論文を出すかもしれない)。
測定した回数が増えると、
それぞれの実験間で比較をしたいケースが増える。
ノンリニア法は、そのペア以外のデータとの比較を保証しないので、
そのたびに補正をしなおす必要がある。
これをなおざりにすると解析結果に矛盾が蓄積する。
比較ごとに計算した結果が一般性を持たないので、
知見をとりまとめることができない。
多くの研究者が、
レシオデータが、シグナルの強度にかかわらず
一定の平均値(=0)をもつこと
という視点を妥当性の検証に用いていた。
もちろんこの視点には
生物学的な裏づけとなる事実がなかったのだが(今はある)、
てっとり早くこれを実現するために
補正用の関数を導入してしまったその考え方は、
恣意的であるという誹りを免れない。
そこで、その視点からの妥当性の検証が原理的に不可能である。
そうなるように補正できる方法で、
そうなるように補正したので、
そうならないわけがないからだ。
実際には別の視点から妥当性は検証できる。
そのひとつが、
レシオデータのふれ巾が、
シグナルの強度にかかわらず一定になること
である。これについても、生物学的な裏づけが、すでに得られている。
ノンリニア法は、この要件を満たさない。
そこで、標準化法としては妥当でない。
良分散安定化法にしても、ANOVA法にしても、
恣意的であるとまで糾弾されるほどの欠陥はないと思われる。
分散安定化法は補正計算が込みいっていて、
そしてレシオに対応しない問題をもち、
ANOVA法はノイズに弱く、
再計算が手間であるという欠点を持つが、
少なくともこれらはランク−ログレシオプロットなどで
その妥当性を確認できる。
その最大の問題点は、確認した妥当性が、芳しくないことだろう。
| Go Back | home | top | トランスクリプトーム研究の目次 |